Poincaré inequality
In mathematics, the Poincaré inequality is a result in the theory of Sobolev spaces, named after the French mathematician Henri Poincaré. The inequality allows one to obtain bounds on a function using bounds on its derivatives and the geometry of its domain of definition. Such bounds are of great importance in the modern, direct methods of the calculus of variations. A very closely related result is the Friedrichs' inequality.
Contents |
Statement of the inequality
The classical Poincaré inequality
Assume that 1 ≤ p ≤ ∞ and that Ω is a bounded connected open subset of the n-dimensional Euclidean space Rn with a Lipschitz boundary (i.e., Ω is a Lipschitz domain). Then there exists a constant C, depending only on Ω and p, such that for every function u in the Sobolev space W1,p(Ω),
where
is the average value of u over Ω, with |Ω| standing for the Lebesgue measure of the domain Ω.
Generalizations
There exist generalizations of the Poincaré inequality to other Sobolev spaces. For example, the following (taken from Garroni & Müller (2005)) is a Poincaré inequality for the Sobolev space H1/2(T2), i.e. the space of functions u in the L2 space of the unit torus T2 with Fourier transform û satisfying
there exists a constant C such that, for every u ∈ H1/2(T2) with u identically zero on an open set E ⊆ T2,
where cap(E × {0}) denotes the harmonic capacity of E × {0} when thought of as a subset of R3.
The Poincaré constant
The optimal constant C in the Poincaré inequality is sometimes known as the Poincaré constant for the domain Ω. Determining the Poincaré constant is, in general, a very hard task that depends upon the value of p and the geometry of the domain Ω. Certain special cases are tractable, however. For example, if Ω is a bounded, convex, Lipschitz domain with diameter d, then the Poincaré constant is at most d/2 for p = 1, d/π for p = 2 (Acosta & Durán 2004; Payne & Weinberger 1960), and this is the best possible estimate on the Poincaré constant in terms of the diameter alone. For smooth functions, this can be understood as an application of the isoperimetric inequality to the function's level sets. [1] In one dimension, this is Wirtinger's inequality for functions.
However, in some special cases the constant C can be determined concretely. For example, for p = 2, it is well known that over the domain of unit isosceles right triangle, C = 1/π ( < d/π where 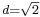 ). (See, for instance,Kikuchi & Liu (2007).)
). (See, for instance,Kikuchi & Liu (2007).)
References
- Acosta, Gabriel; Durán, Ricardo G. (2004), "An optimal Poincaré inequality in L1 for convex domains", Proc. Amer. Math. Soc. 132 (1): 195–202 (electronic), doi:10.1090/S0002-9939-03-07004-7
- Evans, Lawrence C. (1998), Partial differential equations, Providence, RI: American Mathematical Society, ISBN 0-8218-0772-2
- Fumio, Kikuchi; Xuefeng, Liu (2007), "Estimation of interpolation error constants for the P0 and P1 triangular finite elements", Comput. Methods. Appl. Mech. Engrg. 196 (37–40): 3750–3758, doi:10.1016/j.cma.2006.10.029 MR2340000
- Garroni, Adriana; Müller, Stefan (2005), "Γ-limit of a phase-field model of dislocations", SIAM J. Math. Anal. 36 (6): 1943–1964 (electronic), doi:10.1137/S003614100343768X MR2178227
- Payne, L. E.; Weinberger, H. F. (1960), "An optimal Poincaré inequality for convex domains", Archive for Rational Mechanics and Analysis: 286–292, ISSN 0003-9527
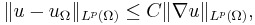
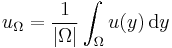
![[ u ]_{H^{1/2} (\mathbf{T}^{2})}^{2} = \sum_{k \in \mathbf{Z}^{2}} | k | \big| \hat{u} (k) \big|^{2} < %2B \infty:](/2012-wikipedia_en_all_nopic_01_2012/I/4bf5bd79e3ea78e00d33bfa1255c536f.png)
![\int_{\mathbf{T}^{2}} | u(x) |^{2} \, \mathrm{d} x \leq C \left( 1 %2B \frac1{\mathrm{cap} (E \times \{ 0 \})} \right) [ u ]_{H^{1/2} (\mathbf{T}^{2})}^{2},](/2012-wikipedia_en_all_nopic_01_2012/I/5fcdf26b722555d66002d13744debfca.png)